A core component of modern transformer-based language models is self-attention. With self-attention, the embedding of a specific token (or word) in a sentence is transformed by the embeddings of surrounding tokens, capturing sentence context. For example, the word "station" has different meanings in the sentences "I am listening to a radio station" and "I just left the train station".
Self-attention by itself is order-agnostic and would compute the same results for the sentence "left train I station the just" or "I just left the train station". This is unfortunate, because word order is important in natural language. So, how do we ensure that self-attention will consider token positions?
Position as a sinusoidal signal
The trick presented in the original "Attention is all you need" paper is to encode the position of a token into the embedding before computing attention values (Vaswani et al. 2017). These position encodings, or positional embeddings, can take various forms, and a popular approach is the sinusoidal positional embedding. The d-dimensional positional encoding for a position n is defined as follows:
$$ r_{ni} = \begin{cases} \sin(\frac{n}{L^{i/d}}) & \text{if } i \text{ is even}\\ \cos(\frac{n}{L^{(i-1)/d}}) & \text{if } i \text{ is odd}\end{cases}$$
Let's plot these values for varying n and i to obtain a better sense of what this encoding represents.
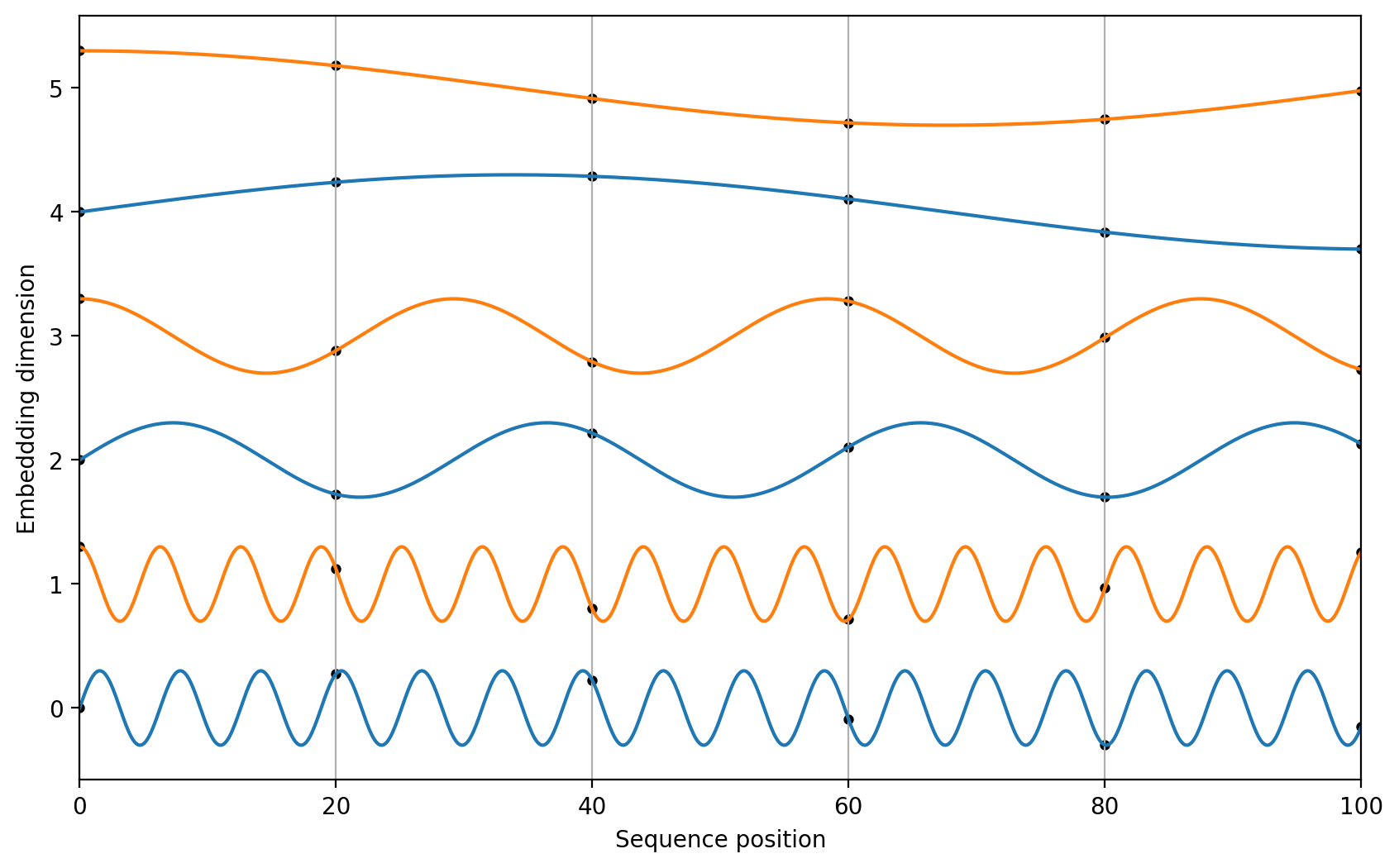
The encoding values lie in the range [-1, 1], with the values in the lower embedding dimensions changing more frequently than those in the higher dimensions. This is similar to binary numbers, where the least significant bits change much more frequently than the most significant bits (Bishop, 2023). This positional embedding vector is then simply added to a token embedding before computing attention:
$$ \textbf{x}_n' = \textbf{x}_n + \textbf{r}_n$$
A downside of this approach is that it encodes the absolute position into the token embedding. In many sequences, the relative ordering of words or tokens is more important. For example, in the sentences "I just left the train station" and "Because I was late, I left the train station," the relationship between "train" and "station" is the same, even though they occur at different absolute positions in each sentence.
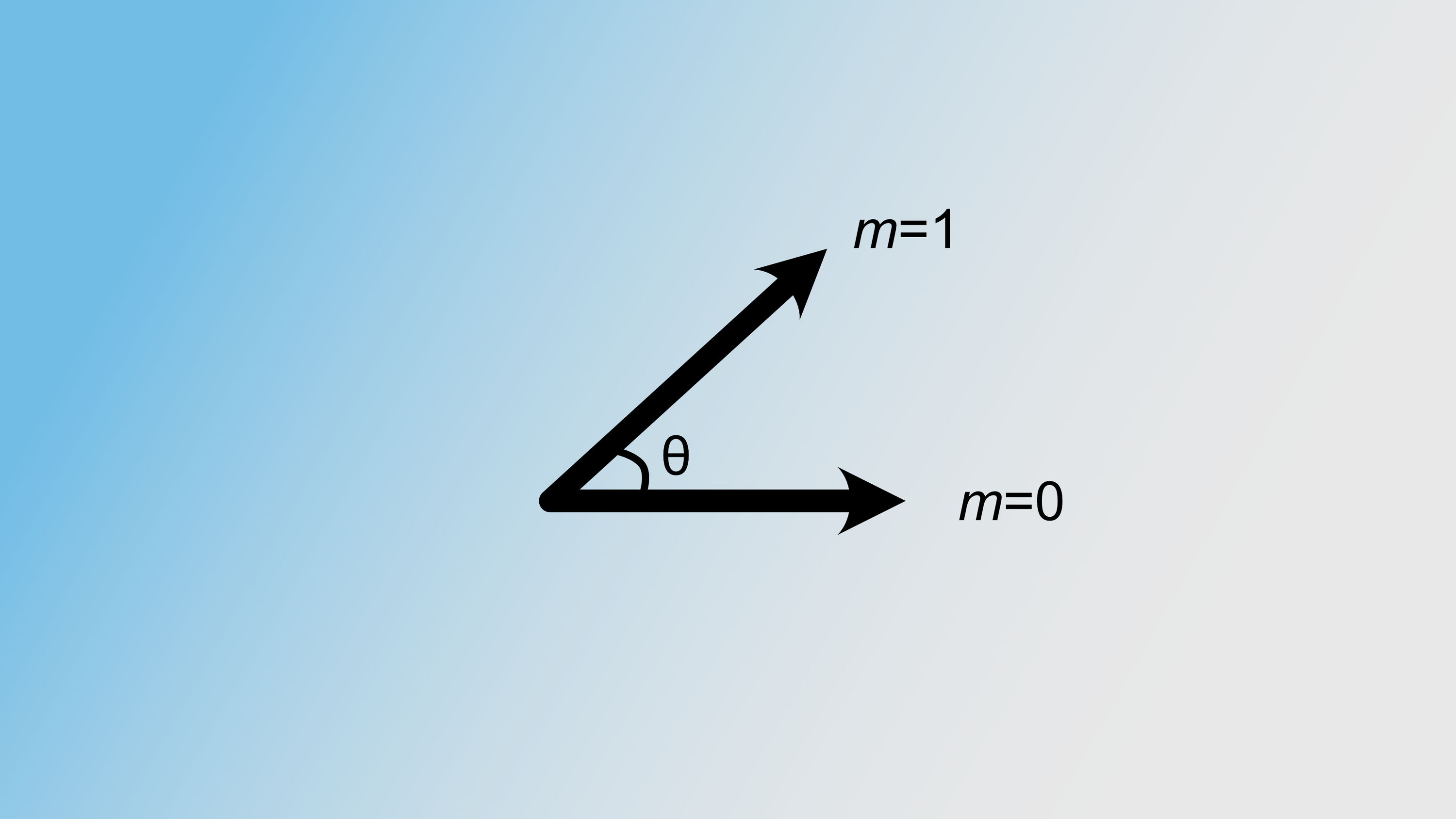
This is where "Rotary Positional Encodings" (RoPE) come in (Su et al. 2023). RoPE similarly uses a sinusoidal signal to encode the position. However, instead of adding this signal to the original input vector, RoPE multiplies the sinusoidal signal with the input after projection into query or key space. For example, to compute a position-adjusted query vector from the original token at position $m$, with the embedding dimension $d=2$:
$$ \textbf{q}' _m = \textbf{R} \textbf{W}_q \textbf{x}_m = \begin{bmatrix} \cos m\theta & -\sin m\theta \\ \sin m\theta & \cos m\theta\end{bmatrix} \begin{bmatrix} W _q ^{11} & W _q ^{12} \\ W _q ^{21} & W _q ^{22}\end{bmatrix} \begin{bmatrix} x _m ^1 \\ x _m ^2\end{bmatrix} $$
Those familiar with linear algebra might recognize the rotation matrix. The input thus gets rotated, with the rotation angle being dependent on the token position $m$. We generalize to embedding dimensions greater than two by expanding matrix $\textbf{R}$ as follows:
$$ \textbf{R}^d = \begin{bmatrix} \cos m\theta_1 & -\sin m\theta _1 & 0 & 0 & \ldots & 0 & 0\\ \sin m\theta _1 & \cos m\theta _1 & 0 & 0 & \ldots & 0 & 0\\ 0 & 0 & \cos m\theta _2 & -\sin m\theta _2 & \ldots & 0 & 0\\ 0 & 0 & \sin m\theta _2 & \cos m\theta _2 & \ldots & 0 & 0\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots\\ 0 & 0 & 0 & 0 & \ldots & \cos m\theta _{d/2} & -\sin m\theta _{d/2}\\ 0 & 0 & 0 & 0 & \ldots & \sin m\theta _{d/2} & \cos m\theta _{d/2}\end{bmatrix}$$
Pairs of features get rotated with varying base frequencies $\theta _i$. $\theta_i$ is defined similarly as in the absolute positional embeddings, with lower embedding dimensions rotating more quickly than higher embedding dimensions:
$$ \theta _i = \frac{1}{L^{2i/d}} $$
The benefit of using rotated vectors is that the angle between two position-adjusted vectors at $m$ and $n$ will only depend on their relative position, not on the absolute positions $m$ and $n$.
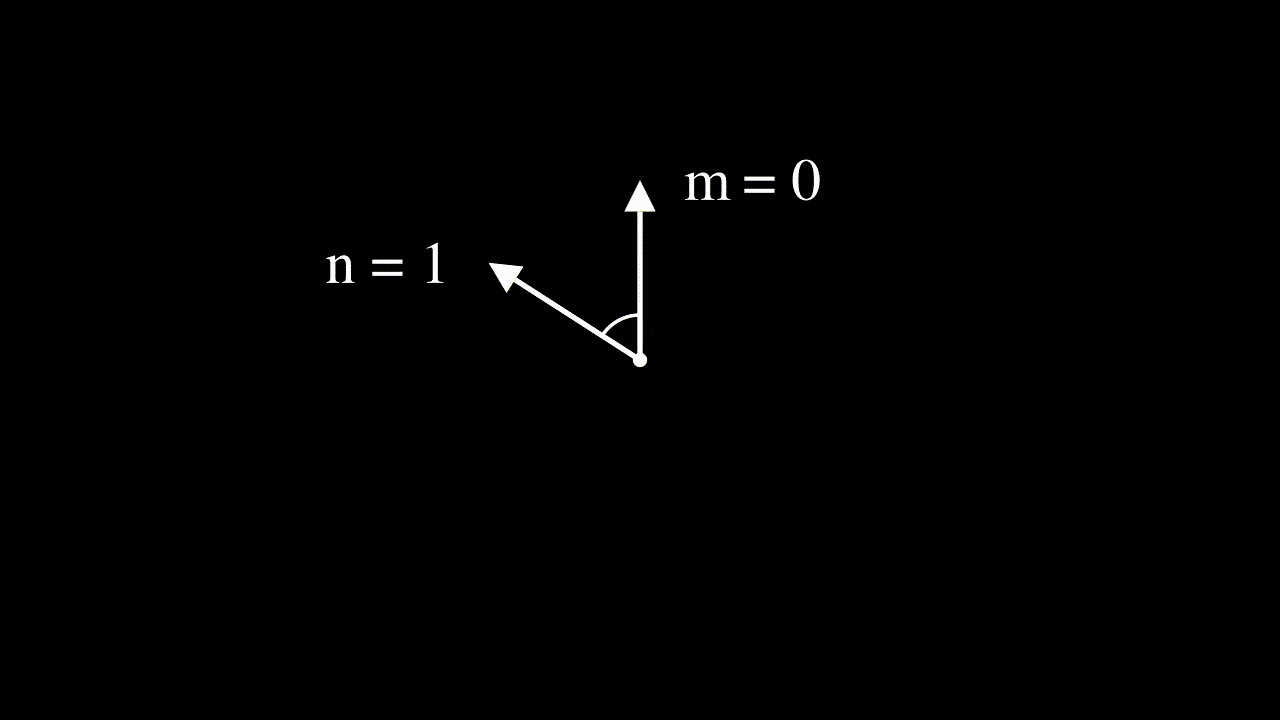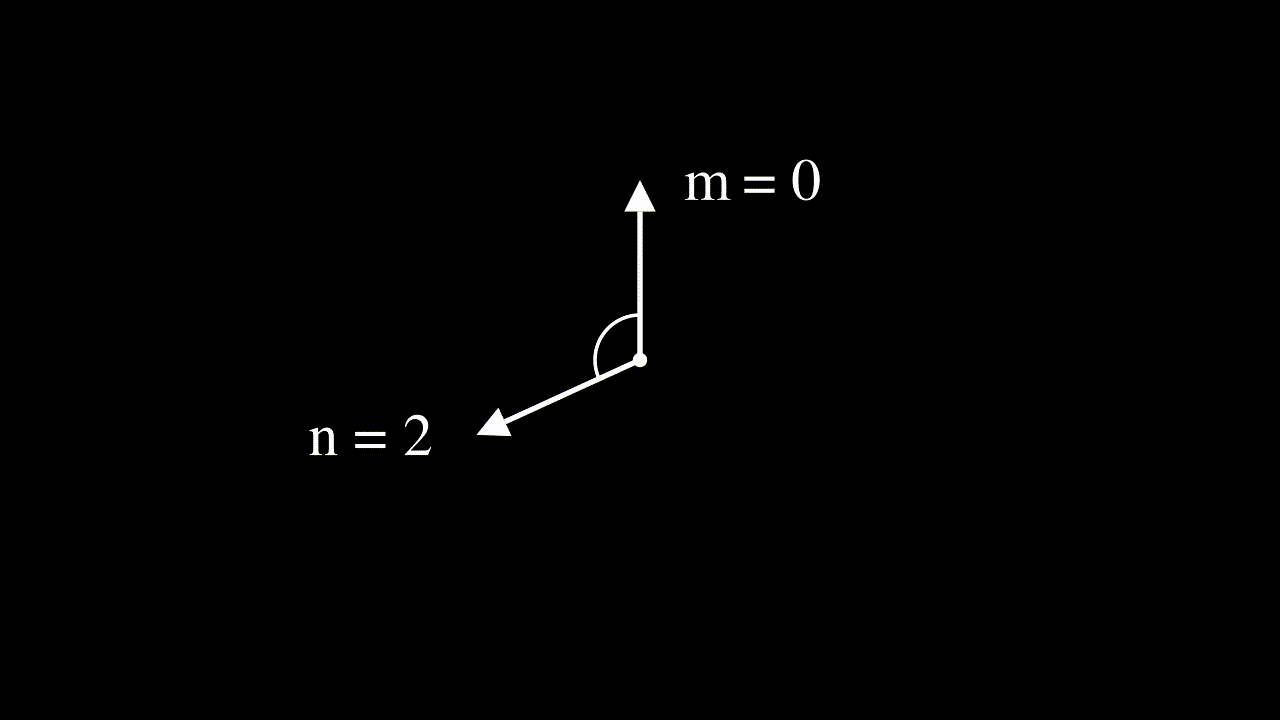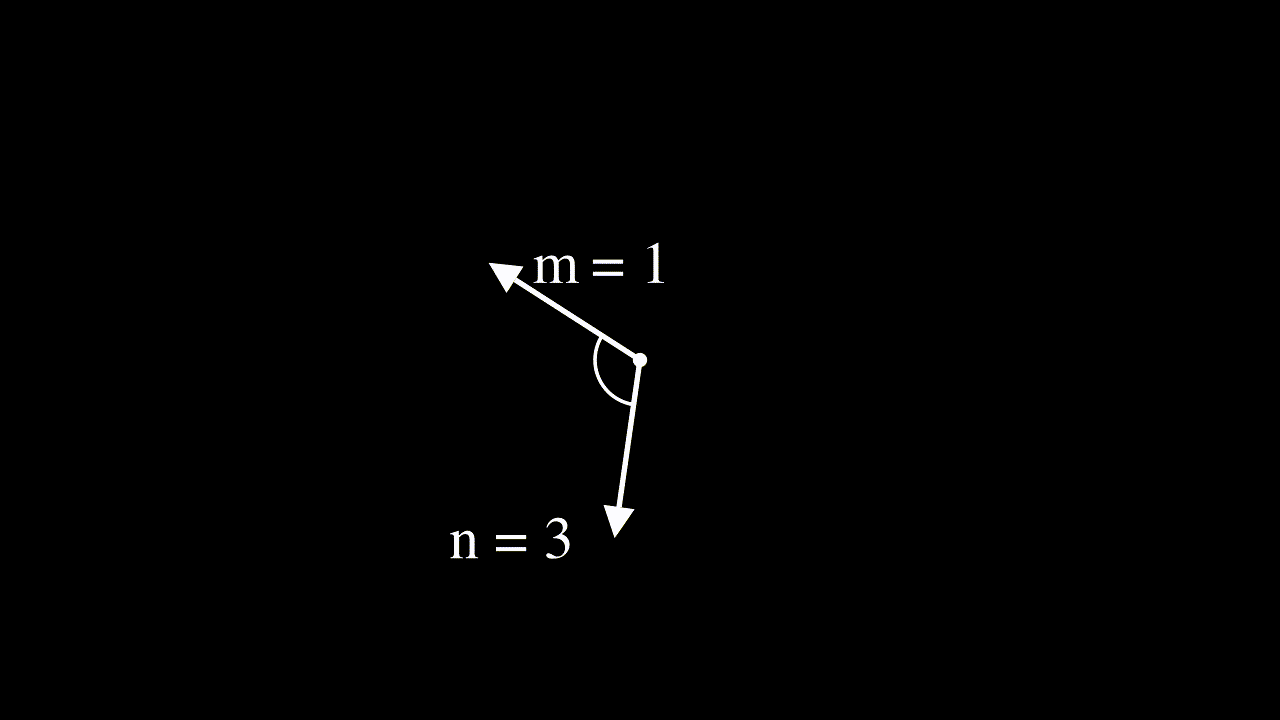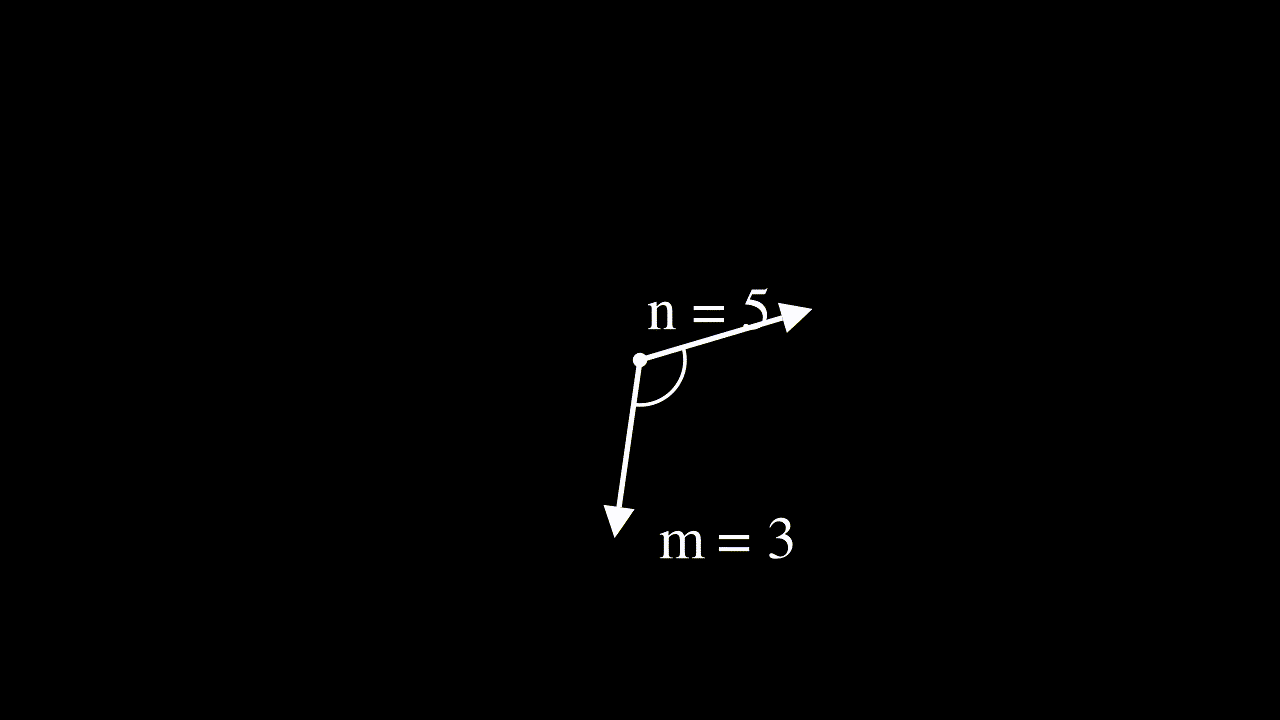
Interpreting input features as complex numbers to derive the RoPE equation
How was RoPE's rotation equation obtained? To explain its derivation, let's recall that the attention weights are computed by taking the softmax of the inner product between query and key vectors. In the case of self-attention, the query and key vectors are derived from different tokens in the sequence:
$$ a_{nm} = \frac{\exp{\langle \textbf{q}_n^{T}, \textbf{k}_m\rangle}}{\Sigma_{m'=1}^N \exp{\langle \textbf{q}_n^{T}, \textbf{k}_{m'}\rangle}} $$
When using absolute positional encodings, the query and key vectors will be derived from the position-adjusted vector $\textbf{x}_n'$. For RoPE, we aim to find an alternative function $f$ to encode positional information, such that the inner product between two position-adjusted vectors only depends on the relative position between two tokens. Mathematically, the following should hold:
$$ \langle f(\textbf{q}, m), f(\textbf{k}, n)\rangle = g(\textbf{q}, \textbf{k}, n - m) \tag{1}$$
To derive such a function, we turn to the complex domain. A d-dimensional vector $\textbf{v}_n \in \mathbb{R}^d$ can be interpreted as a complex (d/2)-dimensional vector $\textbf{v}_n' \in \mathbb{C}^{d/2}$. For example:
$$ \textbf{v}_n = \begin{bmatrix} v_1\\ v_2\\ v_3\\ v_4\end{bmatrix} \rightarrow \textbf{v}_n' = \begin{bmatrix}v_1 + v_2i\\ v_3 + v_4i\end{bmatrix}$$
A complex number $a + bi$ can alternatively be written in polar form $R e^{i\theta}$, where $R$ and $\theta$ are called the radial and angular component of a complex number, respectively, and which are defined as $R = |a + bi| = \sqrt{a^2 + b^2}$ and $\theta = \arctan(b/a)$.
The standard inner product on $\mathbb{C}^d$ is defined as $\langle \textbf{u}, \textbf{v}\rangle = \overline{\textbf{u}}^T\textbf{v}$, i.e., taking the complex conjugate and transpose of $\textbf{u}$ before multiplication with $\textbf{v}$. Using this definition, and writing the complex numbers returned by $f$ and $g$ in polar form, we can obtain the following:
$$ \overline{R_f(\textbf{q}, m) e^{i\Theta_f(\textbf{q}, m)}} \cdot R_f(\textbf{k}, n) e^ {i\Theta_f(\textbf{k}, n)} \\= R_g(\textbf{q}, \textbf{k}, n-m) e^ {i\Theta_g(\textbf{q}, \textbf{k}, n-m)} \tag{2}$$
Here we have explicitly written the inner product between two complex numbers on the left-hand side, equating it to a complex number on the right-hand side, representing $g(\textbf{q}, \textbf{k}, n-m)$. Additionally, we have defined functions $R_f(\textbf{q}, m)$, $\Theta_f(\textbf{q}, m)$, $R_g(\textbf{q}, \textbf{k}, n-m)$, and $\Theta_g(\textbf{q}, \textbf{k}, n-m)$, representing the radial and angular components of the complex numbers returned by $f$ and $g$, respectively.
The conjugate of a complex number in polar form $Re^{i\theta}$ is $Re ^{-i\theta}$. With this definition, we can further simplify the left-hand side of Equation 2 by combining the product of two complex numbers:
$$ R_f(\textbf{q}, m) R_f(\textbf{k}, n) e^{i(\Theta_f(\textbf{k}, n) - \Theta_f(\textbf{q}, m))} = R_g(\textbf{q}, \textbf{k}, n-m) e^{i\Theta_g(\textbf{k}, \textbf{q}, n-m)} \tag{3}$$
Equating the radial and angular components in Equation 3, we obtain:
$$ R_f(\textbf{q}, m) R_f(\textbf{k}, n) = R_g(\textbf{q}, \textbf{k}, n-m) \\ \Theta_f(\textbf{k}, n) - \Theta _f(\textbf{q}, m) = \Theta_g(\textbf{q}, \textbf{k}, n-m) $$
To make functions $R_f$ and $R_g$ more concrete, we start with a few simple initial conditions. Let's require that a token at the start of a sequence is unmodified by our positional embedding: $f(\textbf{v}, 0) = \textbf{v}$. Here $\textbf{v}$ can refer to $\textbf{q}$ or $\textbf{k}$. Additionally, we define $\textbf{v} = ||\textbf{v}|| e^{i\theta_v} = R_f(\textbf{v}, 0) e^{i\Theta_f(\textbf{v}, 0)}$, i.e., $R_f(\textbf{v}, 0) = ||\textbf{v}||$, and $\Theta_f(\textbf{v}, 0) = \theta_v$, where $\theta_v$ is the angular component of $\textbf{v}$, i.e., the angular component of the reinterpreted values of $\textbf{q}$ or $\textbf{k}$ as a complex number.
Now, let's assess the case when $n=m$:
$$ R_f(\textbf{q}, m) R_f(\textbf{q}, m) = R_g(\textbf{q}, \textbf{k}, 0) = R_f(\textbf{q}, 0) R_f(\textbf{k}, 0) = ||\textbf{q}|| ||\textbf{k}|| \tag{4}$$
Here, we have applied Equation 3 to obtain the result $R_g(\textbf{q}, \textbf{k}, 0)$, and applied it another time to obtain $R_g(\textbf{q}, \textbf{k}, 0) = R _f(\textbf{q}, 0) R _f(\textbf{k}, 0)$. We use our initial condition definitions to obtain the final result.
Note that Equation 4 should hold for all token positions $m$; the final result, however, doesn't depend on $m$. Thus the general solution for $R_f(\textbf{x}, m) = ||\textbf{x}||$.
What can we infer for the radial component when $n=m$? Applying Equation 3 similarly to what we did for the radial component, we obtain:
$$ \Theta_f(\textbf{k}, m) - \Theta _f(\textbf{q}, m) = \Theta _g(\textbf{q}, \textbf{k}, 0) = \Theta _f(\textbf{k}, 0) - \Theta _f(\textbf{q}, 0) = \theta_k - \theta_q \tag{5}$$
Rearranging terms of the first and last components of Equation 5, we obtain:
$$ \Theta_f(\textbf{k}, m) - \theta_k = \Theta_f(\textbf{q}, m) - \theta_q $$
This holds for all $\textbf{q}, \textbf{k}$ and $m$, which implies that the change in the angular component of the position-adjusted complex number is independent of the $\textbf{q}$ or $\textbf{k}$.
This insight gives us some freedom to define $\Theta_f(\textbf{v}, m)$. For example, we can define it as follows:
$$ \Theta_f(\textbf{v}, m) = \theta_v + \phi(m) $$
In other words, we simply add a position-dependent value $\phi(m)$ to the original angular component $\theta_v$. But what would $\phi(m)$ be? We can gain some insight by analyzing the difference between two subsequent positions, i.e., the case when $n = m +1$.
$$ \Theta_f(\textbf{k}, m+1) - \Theta _f(\textbf{q}, m) = \theta _k + \phi(m+1) - \theta_q - \phi(m) \\ \Theta _f(\textbf{k}, m+1) - \Theta _f(\textbf{q}, m) + \theta_q - \theta_k = \phi(m+1) - \phi(m)\\ \Theta _g(\textbf{q}, \textbf{k}, 1) + \theta_q - \theta_k = \phi(m+1) - \phi(m)$$
Here we moved $\theta_q$ and $\theta _k$ to the left-hand side to obtain an expression for $\phi(m+1) - \phi(m)$. Furthermore, by applying Equation 3, we transformed the left-hand side to an expression that does not depend on $m$. This implies that the difference $\phi(m+1) - \phi(m)$ does not depend on $m$ either, and can be constant. We can define $\phi(m)$ as a simple arithmetic progression:
$$ \phi(m) = m\theta + \gamma$$
In this definition, $\theta$ and $\gamma$ are free to choose. For example, we can set $\theta$ to an embedding-dimension-specific value, and set $\gamma = 0$.
Combining all pieces, we arrive at the following:
$$ R_f(\textbf{v}, m) = ||\textbf{v}||\\\Theta _f(\textbf{v}, m) = \theta _v + m\theta\\ f(\textbf{v}, m) = ||\textbf{v}||e^{i\theta _v + m\theta} = \textbf{v}e^{im\theta}$$
Through our constraint on relative position and a few simple initial conditions, we were able to define a simple expression that encodes the sequence position into a query or key vector. Finally, using Euler's formula, we obtain the rotation matrix we discussed at the beginning of this post:
$$ \begin{aligned}e^{im\theta} &= \cos m\theta + i\sin m\theta = \cos m\theta \begin{bmatrix}1 & 0\\0 & 1\end{bmatrix} + \sin m\theta \begin{bmatrix} 0 & -1 \\1 & 0\end{bmatrix} \\&= \begin{bmatrix} \cos m\theta & -\sin m\theta\\ \sin m\theta & \cos m\theta\end{bmatrix}\end{aligned} $$
Conclusion
Token order is critical for accurately interpreting natural language and biological sequences. By constraining the inner product between position-adjusted query and key vectors to be only dependent on their relative position, RoPE derives a simple transformation, rotating input vectors in the complex domain. This ensures the attention weights for two tokens are also influenced by their relative position.
References
Bishop, C. M., Bishop, H. & Cham, S. (ed.) (2023). Deep Learning - Foundations and Concepts. ISBN: 978-3-031-45468-4
Su, Jianlin, Yu Lu, Shengfeng Pan, Ahmed Murtadha, Bo Wen, and Yunfeng Liu. “RoFormer: Enhanced Transformer with Rotary Position Embedding.” arXiv:2104.09864. Preprint, arXiv, November 8, 2023. https://doi.org/10.48550/arXiv.2104.09864.
Vaswani, Ashish, Noam Shazeer, Niki Parmar, et al. “Attention Is All You Need.” arXiv:1706.03762. Preprint, arXiv, August 2, 2023. https://doi.org/10.48550/arXiv.1706.03762.